题目描述

安东诺夫的庄园里面有一个很大很大的城堡，上面有一幅壁画。

壁画你可以大概理解为一个平面直角坐标系，并且上面还画着三种直线：

• $x\ =\ n$ ($n$ 为整数)
• $y\ =\ n$ ($n$ 为偶数)
• $x\ +\ y\ =\ n$ ($n$ 为偶数)

每个分割出来的区域都有黑白中的一种颜色，且相邻区域颜色不同。且包含点 $(0.5,0.5)$ 的区域为黑色。壁画如下图。

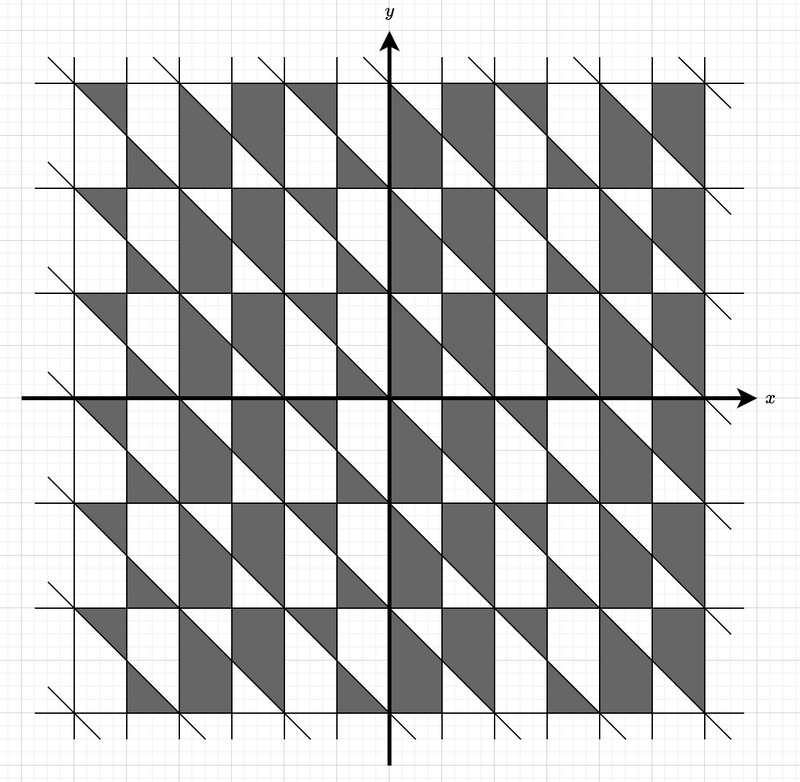
安东诺夫想在壁画上面取出一个长方形，且边都平行于坐标轴，其中左下角的坐标是 $(A,B)$，右上角的坐标是 $(C,D)$。现在你要求为黑色区域的面积。当然，为了输出方便，最后你需要输出面积 *2 的结果。

输入格式

输入只有四个数，分别是 $A,B,C,D$。

输出格式

只有一个数，为黑色区域面积 * 2 的结果。

0 0 3 3

10

-1 -2 1 3

11

-1000000000 -1000000000 1000000000 1000000000

4000000000000000000

数据范围

• $-10^9\ \leq\ A,\ B,\ C,\ D\ \leq\ 10^9$
• $A\ <\ C$ 且 $B\ <\ D$
• 输入的都是整数